LeetCode 62. Unique Paths

Description

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

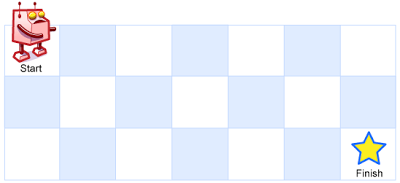
Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

Constraints:

• 1 <= m, n <= 100
• It’s guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

Explanation

We can use a two-dimensional array to show the number of unique paths to each square on the grid.

The number of unique paths to each square on the left border would be 1.

The number of unique paths to each square on the top border would be 1.

The number of unique paths to other squares on the left border would be the sum of the number of unique paths to its previous left square and top square.

Java Solution

class Solution {
    public int uniquePaths(int m, int n) {
        if (m == 0 || n == 0) {
            return 0;
        }
        
        int[][] numberOfPaths = new int[m][n];
        
        for (int i = 0; i < m; i++) {
            numberOfPaths[i][0] = 1;
        }
        
        for (int j = 0; j < n; j++) {
            numberOfPaths[0][j] = 1;
        }
        
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                numberOfPaths[i][j] = numberOfPaths[i - 1][j] + numberOfPaths[i][j - 1];
            }
        }
        
        return numberOfPaths[m - 1][n - 1];
        
        // Time Complexity: O(m * n)
        // Space Complexity: O(m * n)        
    }
}

Python Solution

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        
        dp = [[0 for j in range(0, n)] for i in range(0, m)]
            
        for i in range(0, m):
            dp[i][0] = 1
        
        for j in range(0, n):
            dp[0][j] = 1
            
        for i in range(1, m):            
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
                
        
        return dp[m - 1][n - 1]

• Time complexity: O(N×M).
• Space complexity: O(N×M).